Math in a recursive trolley problem

A while back, as I was mindlessly scrolling through my twitter feed, I had happened to stumble upon the following image.

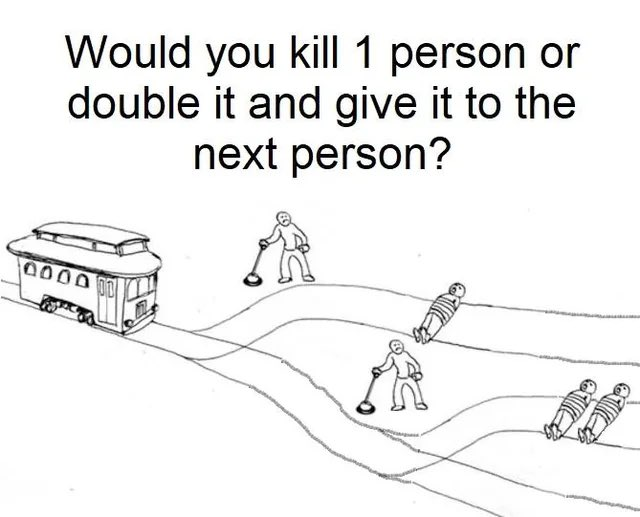
Normally these kind of images I glance over once before immediately forgetting, but this one had happened to get me thinking, what is the optimal strategy here?

The image doesn't show this, but it does imply that if the one death is doubled and given to the next person, they will be faced with a choice between killing two people, or doubling that and giving a choice between 4 people and doubling to the next person on, continuing infinitely. Hypothetically, if perfect cooperation is used, one can simply trust all of the infinite people ahead of them to not ever choose to kill. This requires complete trust in an infinite number of people, but given they all do as you expect, it'll yield 0 deaths, as the amount of people on the other track are always doubled, but are never once chosen to be ran over.

After five lever pulls, the amount of people on the other track would have reached 32. After 10, it would be 1024. After 33 lever pulls, the toll would be about 8.5B, more people than there are on earth. The implication with this being that pulling the lever will cause everyone on earth, including the one pulling the lever, to die instantly. The psychology of the problem changes dramatically, even after 15 pulls. While people may be able to rationalise killing 1 person in exchange for 5, a very, very large majority of people will not want to kill the entire human race. After the 33rd lever pull, every subsequent lever pull will practially be "Hey, do you want to kill everyone in existence? No? Alright, I'll just go ask someone else." As such, the probability of anyone not pulling the lever would very dramatically go down.

The key phrase here is "Very dramatically go down", as opposed to becoming zero. While the probability that asking a random person if they would want to kill everyone instantly and them earnestly replying that they would is very, very low, we all know damn well that someone out there would do it. But the chance that you'd find someone who would would be so low that that wouldn't matter, right?

Say you defined the chance of any given person wanting to kill everyone as the probability of an event: P(k). k in this case is the event that someone would pull the lever that kills everyone. Let's set P(k) to a ludicrously small value.

\[P(k) = {10^{-9}}\]

This value, in layman's terms, is one billionth. It is the same probability as rolling a 10 sided dice and having it land on 10 9 times without error. This is just an estimate, albeit a fairly pessimistic one, but watch what happens next:

\[P(k') = {1-10^{-9}}\]

This represents the probability of someone not wanting to kill everyone on the planet. it is an incredibly high probability, nearly guaranteed for any individual.

Chances are that if you're on this site you definitely know this, but I might as well explain what I'm about to do next. The probability of two unrelated events happening simultaneously can be calculated by muliplying the probabilities of each event together. If the chance of a coin landing on heads is 1/2 and the chance of a dice landing on 6 is 1/6, the chance of both happening at once is 1/12. If I multiply an event by itself a number times, you can calculate the chance of that event occuring that many times in a row. I am going to raise the value of P(k') to the power of the number of people on the planet, (8,040,072,255 as of writing this.) This should yield the probability of everyone on the planet simulaneously agreeing to not end life on earth.

\[P(k')^{8,040,072,255} = (1-{10^{-9}})^{8,040,072,255}=0.0003222856612315605922253392488815511344339451506492181778478939\]

This value is just over 3/10,000. Not the best of odds, really. That's assuming everyone chooses as intended too. This doesn't account for if people trip up and don't pull the lever by accident, misinterpret how the lever works, or cannot pull the lever. That's not even mentioning all the literal toddlers and 14 year olds who'll be trusted with this.

From this knowledge, it can be intepreted that not pulling the lever initially and letting 1 person die will have potentially infinitely less consequences than not pulling the lever. I would write more, but for a first post i'm fairly satisfied and also its like 1 AM so probably better if I elaborated on this later. Toodeloo.